Unliked value-based methods, policy optimization methods search over policy parameters without computing structured value representations for states (or state-action pairs), in order to find parameters that maximize (or minimize) a policy objective function.

Let $U (θ)$ be any policy objective function. Then the general structure would follow something like

Initialize policy parameters $θ$
Sample trajectories $τ_{i} = {s_{t}^{i}, a_{t}^{i}}_{t = 0}^{T}$ by deploying the current policy $π_{θ} (a_{t} ∣ s_{t})$
Compute gradient vector $\nabla_{θ} U (θ)$ Typically this is done through estimation from collected data.
Apply a gradient ascent update $θ \leftarrow + α \nabla_{θ} U (θ)$

In comparison to value-based methods, policy-based methods are

more effective in high-dimensional + continuous action spaces Value-based methods should generally select optimal actions based on something like $\arg max_{a} Q (s, a)$ that faces problems across high dimensions.
better at learning stochastic policies Policy-based methods are naturally stochastic: this is because our policy parameters $θ$ parameterize a distribution that our actions are sampled from. Remember that value-based methods need to rely on heuristics like epsilon-greedy to embed exploration in their policies.

Why is stochasticity a good thing?
- exploration is optimal to train any policy
- in partial-observability settings/environments, deterministic mappings aren’t the only optimal solution

Evolutionary Methods for Policy Search

These are called evolutionary methods because they closely follow the evolution of a population!

Initialize a population of parameter vectors Genotypes
Make random permutations to each parameter vector Simulate mutations in offspring
Evaluate the perturbed parameter vector
Update your policy parameters to move to favor the best performing parameter vectors Survival of the fittest enabling fitness in this offspring

These are examples of black-box policy optimization, where we treat the policy and environment as a “black box” that we can query (run rollouts) and update our policy based purely on performance we can observe;

we do not learned a structured “state” representation of state values and/or state-action values based on the structure of Bellman equations
use gradients to update policy parameters directly like in policy gradient methods, but may do so indirectly like in NES

CEM: Cross-Entropy Method

In this method, we

sample $n$ policy parameters $θ_{i}$ from a multivariate Gaussian distribution matrix $p_{ϕ} (θ)$
Evaluate those $n$ parameters to generate a reward signal or scalar return $F (θ_{i})$
select a proportion $ρ$ of those parameters with highest score as our elite samples
use their corresponding $μ$ and $σ^{2}$ to update our reference matrix for sampling, which basically means setting the new mean as the mean of those highest $ρ n$ parameters and setting the new variance as simply the variance of those selected elite samples!

This worked really well up to the 2010’s and in low dimensional search space dimensions, shown to work well in Tetris (Szita, 2006), where we can craft a state-value function that is a linear combination of 22 basis functions $ϕ (s)$ (individual column heights, height differences, etc)

V_{w} (s) = \sum_{i = 1}^{22} w_{i} ϕ_{i} (s)

These evolutionary search methods weren’t a threat to DQN implementations at the time because they couldn’t scale to large non-linear neural nets with thousands of parameters.

CMA-ES: Covariance Matrix Adaptation

Instead of limiting ourselves to diagonal Gaussian, we search by learning a full covariance matrix so instead of just updating the mean and variances, we’re updating the full covariance matrix.

Visually, if there is an objective function we are trying to reach that is best maximized with samples in a 2d rotated ellipse, then we should utilize all the entries in a full covariance matrix which then allows us to rotate a standard diagonal gaussian matrix (x-y aligned ellipse) to best maximize this objective function efficiently.

NES - Natural Evolutionary Strategies

NES considers every offspring when updating our policy parameters - they optimize our expected fitness objective by updating the parameters of our search distribution through a natural gradient, specifically updating our learned mean $μ$ , while fixing our covariance this time.

Consider the parameters of our policy $θ \in R^{d}$ are sampled from a Gaussian distribution with learned mean $μ \in R^{d}$ and fixed diagonal covariance matrix $σ^{2} I$ (which is not being learned). We denote this distribution as $P_{μ} (θ)$

θ \sim P_{μ} (θ) = N (μ, σ^{2} I)

Our goal is find the best possible policy distribution, parameterized by $μ$ , that our policy is sampled from (through $θ$ )

max_{μ} E_{P_{μ} (θ)} F (θ)

based on a fitness score which is the expectation of reward over entire trajectories

F (θ) = E_{τ \sim π_{θ}, s_{0} \sim μ_{0} (s)} R (τ)

Deriving the Natural Gradient

Computing the update for our mean $μ$ through this objective is as follows:

\begin{aligned} (use p.m.f to integrate out expectation) & \nabla_{μ} E_{θ \sim P_{μ} (θ)} [F (θ)] & = \nabla_{μ} \int P_{μ} (θ) F (θ) d θ \\ = \int \nabla_{μ} P_{μ} (θ) F (θ) d θ & = \int P_{μ} (θ) \frac{\nabla_{μ} P_{μ} (θ)}{P_{μ} (θ)} F (θ) d θ \\ (derivative of log trick!) & = \int P_{μ} (θ) \nabla_{μ} \log P_{u} (θ) F (θ) d θ \\ (based on pmf) & = E_{θ \sim P_{μ} (θ)} [\nabla_{μ} \log P_{μ} (θ) F (θ)] \\ (Monte Carlo Sampling) & \approx \frac{1}{N} [\nabla_{μ} \log P_{μ} (θ) F (θ)] \\ (\log P_{μ} (θ) = - \frac{∥ θ - μ ∥}{2 σ^{2}} + C for Gaussians) & \approx \frac{1}{N} [\sum_{i = 1}^{N} \frac{θ - μ}{σ^{2}} F (θ)] \\ (Reparameterization trick for θ) & \approx \frac{1}{N} [\sum_{i = 1}^{N} \frac{ϵ}{σ} F (θ)] \end{aligned}

From this derivation, we have shown that this gradient can be estimated by

sampling $N$ parameters $θ_{i}$ , running trajectories for each parameter, and obtaining our scalar fitness score $F (θ_{i})$ for each sample
Then we simply need to scale by a sampled noise term $ϵ$ divided by our variance $σ$ and average out all scaled terms!

To expand on that last step, in order to back propagate through Gaussian distributions to $μ$ , then the sampling of $θ_{i} \sim N (μ, σ^{2} I)$ needs to be converted through the reparameterization trick so that $θ_{i} = μ + σ ϵ_{i}, ϵ_{i} \sim N (0, I)$ .

Based on this derivation we can now apply gradient ascent to iteratively update our $μ$ ! (based on learning rate $α$ )

μ_{t + 1} = μ_{t} + α [\frac{1}{n σ} \sum_{i = 1}^{n} ϵ_{i} F (θ_{i})]

Black-Box Optimization

To clarify, this is still black-box optimization:

We do not need to know anything about how we are computing our fitness score, we are simply using raw output returns given our samples $θ_{i}$
We are not computing computing analytic gradients of $F (θ)$ wrt to $θ$ in order to update our policy parameters directly; in fact, we compute gradients wrt to a different, known object that we have set: the search distribution $P_{μ} (θ)$

Scalability + Parallelization of ES

The reason why this scales well for large dimension $θ$ when we are working with large neural networks is that when parallelizing this natural gradient computation across multiple worker processes, then each worker needs to compute this term $ϵ_{i} F_{i} (θ_{i})$ . This means we need to distribute back and forth this large $θ_{i} = μ_{t} + σ ϵ_{i}$ vector across all our $n$ workers and can do so through

Coordinator broadcasts $μ_{t}$ once per update step to all workers
Coordinator sends $ϵ_{i}$ to all $n$ workers individually, which allows every worker to compute $θ_{i}$
Each workers runs trajectories and sends back $F (θ_{i})$ to the central workers.

Because of reparameterization only this $ϵ_{i}$ needs to be sent back and forth, but this is still a very large parameter, so instead we use a pseudo random number generator to compute $n$ (tiny) seeds and then send these small seeds to the $n$ workers, which can they reconstruct each large dimension $ϵ_{i}$ and compute our returns $F (θ_{i})$ which is just a scalar! So communication time is cut a lot.

Local Maxima Issue

In order to prevent ES methods from getting stuck in local optima, we average our search over multiple tasks and related environments to improve robustness and our objective can become more more generalizable.

Policy Gradient

We no longer consider black-box optimization methods. Instead of updating a search distribution that our policy parameters are sampled from, we directly update our policy parameters, because we need to compute analytic gradients directly!

Policy Objective

One reasonable policy objective is to maximize our expected trajectory reward over distribution of all trajectories parametrized by our policy parameters $θ$ (assuming a discrete trajectory space).

max_{θ} . U (θ) = E_{τ \sim P_{θ} (τ)} [R (τ)] = \sum_{τ} P_{θ} (τ) R (τ)

Remember that $P_{θ} (τ)$ is the probability distribution over seeing that entire trajectory when we run $π_{θ}$ in our environment which abstracts three key ingredients

the initial state being sampled from an initial state distribution
the stochasticity of the policy in which actions are sampled from - this is what our $θ$ actually parameterizes.
the dynamics of the environment resulting in stochastic next states $s_{t + 1}$

P_{θ} (τ) = \underset{initial state}{\underset{⏟}{ρ_{0} (s_{0})}} \prod_{t = 0}^{T} \underset{dynamics}{\underset{⏟}{P (s_{t + 1} ∣ s_{t}, a_{t})}} \underset{action sampling}{\underset{⏟}{π_{θ} (a_{t} ∣ s_{t})}}

It’s assumed that $P$ is a probability density function that is continuous and differentiable - necessary to propagate our gradient as we will see in the derivation.

We now need to figure out how to compute this gradient in order to find optimal $θ$ :

Finite-Difference Methods

One way to try and approximate policy gradient of $π_{θ} (s)$ by nudging $θ$ in every possible small amount dimension and approximate partial derivatives as such:

\frac{\partial U (θ)}{\partial θ_{k}} = \frac{U (θ + ϵ u_{k}) - U (θ - ϵ u_{k})}{2 ϵ}

This was used to train these AIBO robots to walk. But this is really not feasible in high dimensions

Derivatives of the Policy Objective

Policy gradients aim to exploit our factorization of $P_{θ} (τ) = \prod_{t = 0}^{H} P (s_{t + 1} ∣ s_{t}, a_{t}) π_{θ} (a_{t} ∣ s_{t})$ to compute approximate gradient estimate for

\nabla_{θ} U (θ) = \nabla_{θ} E_{τ \sim P (τ; θ)} [R (τ)]

In comparison to evolutionary methods, here the challenge is to compute derivatives w.r.t variables that parameterize a distribution that our expectation is summed over. The derivation uses the same log probability trick as derived for evolutionary methods; also we assume discrete trajectory space to sum over - if continuous, the derivation is largely the same but the justification for moving gradients inside the integral terms is different and above my math knowledge.

\begin{aligned} (expand expectation using pmf) & \nabla_{θ} E_{τ \sim P_{θ} (τ)} [R (τ)] & = \nabla_{θ} \sum_{τ} P_{θ} (τ) R (τ) \\ (sum rule) & = \sum_{τ} \nabla_{θ} P_{θ} (τ) R (τ) \\ (prep for log prob trick) & = \sum_{τ} P_{θ} (τ) \frac{\nabla_{θ} P_{θ} (τ)}{P_{θ} (τ)} R (τ) \\ (chain rule) & = \sum_{τ} P_{θ} (τ) [\nabla_{θ} \log P_{θ} (τ)] R (τ) \\ = E_{τ} [\nabla_{θ} \log P_{θ} (τ) R (τ)] \end{aligned}

I think this part is intuitively explainable, our policy objective gradient is equivalent to increasing the log probability of trajectories that give a positive reward and decreasing the log probability of trajectories that give a negative reward.

The key observation is that this expectation can be simplified much further because our trajectories do encapsulate the dynamics of the environment - but this is not specifically parametrized by our policy parameters, so the derivatives of our trajectories propagate to derivatives of taking actions under our policy.

\begin{aligned} (factorizing our trajectory) & \nabla_{θ} \log P_{θ} (τ) & = \nabla_{θ} \log [ρ (s_{0}) \prod_{t = 0}^{T} P (s_{t + 1} ∣ s_{t}, a_{t}) π_{θ} (a_{t} ∣ s_{t})] \\ (using logs to sum out product!) & = \nabla_{θ} [\log ρ_{0} (s_{0}) + \sum_{t = 0}^{T} \log P (s_{t + 1} ∣ s_{t}, a_{t}) + \log π_{θ} (a_{t} ∣ s_{t})] \\ (dynamics in env. are ⊥ of policy parameters!) & = \nabla_{θ} [\sum_{t = 0}^{T} \log π_{θ} (a_{t} ∣ s_{t})] \\ (sum rule) & = [\sum_{t = 0}^{T} \nabla_{θ} \log π_{θ} (a_{t} ∣ s_{t})] \end{aligned}

Then completing our derivation

\begin{aligned} \nabla_{θ} E_{τ \sim P_{θ} (τ)} [R (τ)] & = E_{τ \sim P_{θ} (τ)} [\nabla_{θ} \log P_{θ} (τ) R (τ)] \\ = E_{τ \sim P_{θ} (τ)} [\sum_{t = 0}^{T} \nabla_{θ} \log π_{θ} (a_{t} ∣ s_{t}) R (τ)] \\ (Monte Carlo Estimation!) & \approx \frac{1}{N} \sum_{i = 1}^{N} \sum_{t = 0}^{T} \nabla_{θ} \log π_{θ} (a_{t} ∣ s_{t}) R (τ) \end{aligned}

To approximate the gradient, we use an empirical estimate to from $N$ sampled trajectories!

\nabla_{θ} U (θ) \approx \frac{1}{N} \sum_{i = 1}^{N} \sum_{t = 0}^{T} \nabla_{θ} \log π_{θ} (a_{t} ∣ s_{t}) R (τ)

Computing Policy Gradient

And the natural question is whether the derivative term is computable - which yes it is.

If our action space is continuous, then we our policy network can be gaussian, outputting a mean and standard deviation.
If our action space is discrete, obviously we apply a final softmax layer to output a discrete probability distribution over finite action space. Then for stochasticity, we can query a categorial distribution based on these probabilities for sampling.

Temporal Structures

Can we do better than a standard $R (τ)$ of the entire trajectory for every gradient update? One problem is the issue with scalar $R (τ)$ , why should the action an agent takes at time step $t$ be scaled by the reward trajectory of time steps that occurred before that $[0, t - 1]$ ?

Instead, we should emphasize causality: Only future rewards should be attributed to the action taken at timestep $t$

G_{t} = \sum_{k = t}^{T} γ^{k} R (s_{k}, a_{k})

REINFORCE - Monte Carlo Policy Gradient

The above discussion concludes REINFORCE - the simplest policy gradient also referred to as “vanilla” policy gradient.

Initialize policy parameters $θ$
Sample trajectories ${τ_{i} = {s_{t}^{i}, a_{t}^{i}}_{t = 0}^{T}}$ by deploying the current policy $π_{θ} (a_{t} ∣ s_{t})$
Compute gradient vector $\nabla_{θ} U (θ) \approx \hat{g} = \frac{1}{N} \sum_{i = 1}^{N} \sum_{t = 1}^{T} \nabla_{θ} \log π_{θ} (a_{t}^{(i)} | s_{t}^{(i)}) G_{t}^{(i)}$
Perform Gradient Ascent: $θ \leftarrow θ + α \nabla_{θ} U (θ)$

Baselines with Advantages

Our gradient estimator is unbiased, but still can have high variance

\hat{g} = \frac{1}{N} \sum_{i = 1}^{N} \sum_{t = 0}^{T} \nabla_{θ} \log π_{θ} (a_{t} ∣ s_{t}) G_{t}

One issue with weighting our gradient updates with $G_{t}$ is the following situation:

a state $s_{1}$ has all actions averaging out to a high positive magnitude reward of $4000$
a state $s_{2}$ has all actions averaging out to a negative reward of $- 4000$ Then no matter if we take a very bad action at $s_{1}$ versus a very good action at state $s_{2}$ the state’s baseline level of reward (expectation) is the major scaling factor in our gradient update, not the intention of whether we took a good or bad action in the first place.

To counteract this we should then only consider the trajectory reward above our a constant-term baseline - Advantages - at that state!

\begin{aligned} {\hat{g}}^{'} & = \frac{1}{N} \sum_{i = 1}^{N} \sum_{t = 0}^{T} \nabla_{θ} \log π_{θ} (a_{t} ∣ s_{t}) [G_{t} - b] \\ = \frac{1}{N} \sum_{i = 1}^{N} \sum_{t = 0}^{T} \nabla_{θ} \log π_{θ} (a_{t} ∣ s_{t}) G_{t} - \underset{how does this affect our gradient estimation?}{\underset{⏟}{\frac{1}{N} \sum_{i = 1}^{N} \sum_{t = 0}^{T} \nabla_{θ} \log π_{θ} (a_{t} ∣ s_{t}) b}} \end{aligned}

Actually, this new ${\hat{g}}^{'}$ is still equal to our original $\hat{g}$ because in expectation the baseline term has zero expectation.

\begin{aligned} E_{τ \sim P_{θ} (τ)} [\nabla_{θ} \log P_{θ} (τ) b] & = b \sum_{τ} P_{θ} (τ) \nabla_{θ} \log P_{θ} (τ) \\ = b \sum_{τ} \frac{P_{θ} (τ) \nabla_{θ} P_{θ} (τ)}{P_{θ} (τ)} \\ = b \cdot \nabla_{θ} E_{τ \sim P_{θ} (τ)} [1] = b \cdot 0 = 0 \end{aligned}

And our subtraction of baseline to consider relative reward has effectively reduce the scale of gradient updates quite a bit, thus we minimize variance overall!

Baseline Choices

Constant Baselines using the average return of the policy $b = E [R (τ)]$
Time-dependent Baselines $b_{t} = \sum_{i = 1}^{N} G_{t}^{(i)}$ where we average temporal reward over all trajectories
State-dependent Baselines i.e. value function $b (s_{t}) = V_{π} (s)$

Actor-Critic Methods

Actor-Critic methods build of our state-dependent baselines used in REINFORCE with baselines method where our action advantage is $A^{π} (s_{t}^{i}, a_{t}^{i}) = G_{t}^{(i)} - V_{ϕ}^{π} (s_{t}^{i})$ . But the $G_{t}^{(i)}$ term can have high variance: it’s a single rollout Monte-Carlo return based on our $s_{t}$ and $a_{t}$ and varies from our environment; but doesn’t this sound familiar?

Our returns $G_{t} = \sum_{k = t}^{T} R (s_{k}, a_{k})$ are exactly estimated by our Q-functions $Q^{π} (s, a) = E [G_{t} ∣ s_{t}, a_{t}]$ by definition. Furthermore, however, if our critic function only estimates our value functions $V_{ϕ}^{π} (s)$ already, then we should expand our bellman equations to express Q-functions in terms of value functions: $Q^{π} (s, a) = E [G_{t} ∣ s_{t}, a_{t}] = E [R_{t} + γ G_{t + 1} ∣ s_{t}, a_{t}] = E [R_{t} + V (s_{t + 1}) ∣ s_{t}, a_{t}]$ .

Then our action advantages can be simplified as

A^{π} (s_{t}^{i}, a_{t}^{i}) = G_{t}^{(i)} - V_{ϕ}^{π} (s_{t}) = R (s_{t}^{i}, a_{t}^{i}) + γ V_{ϕ}^{π} (s_{t + 1}^{i}) - V_{ϕ}^{π} (s_{t})

Initialize actor policy parameters $θ$ and critic parameters $ϕ$
Sample trajectories ${τ_{i} = {s_{t}^{i}, a_{t}^{i}}_{i = 0}^{T}}$ by deploying our current policy $π_{θ} (a_{t} ∣ s_{t})$
Calculate value functions $V_{ϕ}^{π} (s)$ through MC or TD estimation
Compute action advantages $A^{π} (s_{t}^{i}, a_{t}^{i}) = G_{t}^{(i)} - V_{ϕ}^{π} (s_{t}^{i})$
$\nabla_{θ} U (θ) \approx \frac{1}{N} \sum_{i = 1}^{N} \sum_{t = 0}^{T} \log π_{θ} (a_{t} ∣ s_{t}) A (s_{t}, a_{t})$
$θ \leftarrow θ + α \nabla_{θ} U (θ)$

In some sense the actor-critic is just “policy iteration” written in gradient form.

We run the policy and collect a series of $N$ trajectories.
Based on the performance, we compute advantages for each time step during each trajectory
Then we update our policy parameters directly using a policy gradient that is computed through these advantages.

A2C - Advantage Actor-Critic

The trajectories we collect arrive sequentially, while stability of training our policy networks require the gradient updates to be decorrelated - a problem we fixed in Q-learning using replay buffers - a solution is A3C by parallelizing the experience collection to multiple agents in order to stabilize training.

Workers run in parallel, computing gradients from their own rollouts, but we batch updates after each worker has finished their process to a combined gradient update step - ensuring consistent /stable gradient updates.

A3C - Asynchronous Advantage Actor-Critic

The natural performance optimization to make is what if the workers worked asynchronously and computed + provided gradient updates without waiting for all workers each iteration.

PPO - Proximal Policy Optimization

PPO is derived from policy improvement logic and more so a approximate policy iteration method than a policy gradient method.

High UTD

Updates to Data (UTD) = \frac{number of gradient updates}{number of env. steps (samples)}

Obviously it seems to us that a high UTD is efficient with collected data - and a bottleneck in RL for complex environments is exactly data collection - so we want to come up with methods that work well with high UTD.

Here’s the issue:

θ \leftarrow θ + α \nabla_{θ} U (θ)

if we apply one gradient update step, then we land on a new policy $π^{'}$ parameterized by $θ^{'}$ . We cannot compute the same policy gradient estimate for $\nabla_{θ} U (θ)$ by reusing the past rollouts (in order to compute the advantages).

This means that forcing a high UTD is a noisy estimate based on limited experience and can result in policy drifts. This is a motivator for PPO and TRPO methods as we discuss, which aim to fix this issue through

Policy Improvement

Performance of Policy

If we quantify the performance of a policy as expected return over all trajectory

J (π) = E [\sum_{t = 0}^{\infty} γ^{t} r (s_{t}, a_{t})] = E_{s_{0} \sim ρ} [V^{π} (s_{0})]

and define a discounted state visitation distribution that weights time spent in a specific state $s$ over all trajectories given a policy $π$

d^{π} (s) = \sum_{t = 0}^{\infty} γ^{t} \underset{π}{Pr} (s_{t} = s ∣ s_{0} \sim ρ)

where

$\underset{π}{Pr}$ specifically refers to probability over policy (all policy-induced randomness)
the sum of all pmfs for $d^{π} (s)$ over all states $\sum_{s} d^{π} (s) = \frac{1}{1 - γ}$
the discounted average of some state-dependent function $f (s)$ over trajectories is equal to the average over state weighted by how often we visit them

\sum_{t = 0}^{\infty} γ^{t} E_{π} [f (S_{t})] = \sum_{t = 0}^{\infty} γ^{t} \sum_{s} f (s) \underset{π}{Pr} (S_{t} = s) = \sum_{s} f (s) \underset{d^{π} (s)}{\underset{⏟}{\sum_{t = 0}^{\infty} γ^{t} \underset{π}{Pr} (S_{t} = s)}}

Performance Difference Lemma

Then we can show that the policy improvement from $π \to π^{'}$ can be written as expected advantage over state visitation distribution and action sampling from our policy.

J (π^{'}) - J (π) = E_{s \sim d^{' π}, a \sim π^{'} (\cdot ∣ s)} [A^{π} (s, a)]

Policy Improvement Formulation

We aim to find the maximum new policy $π^{'}$ which corresponds to an expression

max_{π^{'}} J (π^{'}) = max_{π^{'}} (J (π^{'}) - J (π)) = max_{π^{'}} E_{s \sim d^{' π} (s), a \sim π^{'} (\cdot ∣ s)} [A^{π} (s, a)]

Importance Sampling

But our whole goal for performance is to not sample from $π^{'}$ for the $s, a$ . If we can’t sample from $π^{'}$ (we can but the whole goal is to avoid sampling) of a distribution $p (z)$ , but want to compute an expectation of a function $f (z)$ under that distribution, then importance sampling allows us to sample from a different easier proposal/behavior distribution $q (z)$ then scale using a term called important weight our function values computed from those samples through manipulation:

\begin{array}{r} E_{z \sim p (z)} [f (z)] = \int f (z) p (z) d z = \int q (z) f (z) \underset{weight}{\underset{⏟}{\frac{p (z)}{q (z)}}} d z = E_{z \sim q (z)} [f (z) \frac{p (z)}{q (z)}] \end{array}

which works as long as the denominator isn’t $0$ whenever $p (z)$ is nonzero.

Derivation

Then to apply this trick to our formulation, we aim to express our expectation entirely in terms of $π$ , our first attempt in re-expressing our state visitation distribution in terms of $π$ would be

max_{π^{'}} E_{s \sim d^{' π} (s), a \sim π^{'} (\cdot ∣ s)} [A^{π} (s, a)] = max_{π^{'}} E_{s \sim d^{π} (s), a \sim π^{'} (\cdot ∣ s)} [\frac{d^{π^{'}} (s)}{d^{π} (s)} A^{π} (s, a)]

but calculating state-visitation ratio $\frac{d^{π^{'}} (s)}{d^{π} (s)}$ is hard in itself - because the discounted visitation for $π^{'}$ is unknown - and if we try to estimate this ratio with a large amount of sampling, then because this is a high variance term that could explode in certain states leading to instability in the computation.

PPO fixes this by simply keeping $π$ close to $π^{'}$ so that the state-visitation distribution naturally induces an approximate equality of $d^{π^{'}} \approx d^{π}$ . And we apply the same importance sampling trick for $π^{'} (\cdot ∣ s_{t})$ which note the ration $\frac{π^{'} (\cdot ∣ s_{t})}{π (\cdot ∣ s_{t})}$ is easy to deal with - this is computable from our policy network in a single forward pass!

\begin{aligned} (PPO assumption) & max_{π^{'}} E_{s \sim d^{' π} (s), a \sim π^{'} (\cdot ∣ s_{t})} [A^{π} (s, a)] & = max_{π^{'}} E_{s \sim d^{π} (s), a \sim π (\cdot ∣ s_{t})} [{\frac{d^{π^{'}} (s)}{d^{π} (s)}}^{1} A^{π} (s, a)] \\ = max_{π^{'}} E_{s \sim d^{π} (s), a \sim π (\cdot ∣ s_{t})} [\frac{π (a ∣ s_{t})}{π^{'} (a ∣ s_{t})} A^{π} (s, a)] \end{aligned}

Now, to compute this objective max function, we need to take gradient ascent steps wrt to this object, and rewrite in the same policy gradient form

\begin{aligned} \nabla_{θ^{'}} E_{s \sim d^{π} (s)} E_{a \sim π (\cdot ∣ s)} [\frac{π^{'} (a ∣ s)}{π (a ∣ s)} A^{π} (s, a)] & = E_{s \sim d^{π} (s)} E_{a \sim π (\cdot ∣ s)} [\frac{\nabla_{θ^{'}} π^{'} (a ∣ s)}{π (a ∣ s)} [A^{π} (s, a)] \\ = E_{s \sim d^{π} (s)} E_{a \sim π (\cdot ∣ s)} π^{'} (a ∣ s) [\frac{\nabla_{θ^{'}} \log π^{'} (a ∣ s)}{π (a ∣ s)} [A^{π} (s, a)] \end{aligned}

But we still have this issue of need to have a high UTD and resulting in policy drift. PPO aims to enforce some closeness penalty constraints on how far the new policy $π^{'}$ can drift from $π$ on each gradient update! This is a regularization term.

E_{s \sim d^{π} (s)} E_{a \sim π (\cdot ∣ s)} [\frac{\nabla_{θ^{'}} \log π^{'} (a ∣ s)}{π (a ∣ s)} A^{π} (s, a)] - λ E_{s} [D (π (\cdot ∣ s), π^{'} (\cdot ∣ s))]

Clipped Ratio Objectives

What PPO does is use a soft approximation by utilizing ratio clipping keeping the $\frac{π^{'} (a ∣ s)}{π (a ∣ s)}$ close to 1 instead of using an explicit distance metric (KL Divergence) like with TRPO. Remember the whole purpose is to make sure the old batch is representative of the new policy so we can get high UTD.

This can be expressed as

max_{π^{'}} E_{s \sim d^{π} (s)} E_{a \sim π (\cdot ∣ s)} [m i n (\frac{π^{'} (a ∣ s)}{π (a ∣ s)}, c l i p (\frac{π^{'} (a ∣ s)}{π (a ∣ s)}, 1 - ϵ, 1 + ϵ)) A^{π} (s, a)]

Note that a naive clip objectives clips our ratio on both sides of the curve. But this has the issue of

if our advantage $A > 0$ and our ratio $r < 1 - ϵ$ because the clipped value is flat on this side of the naive clip objective, the gradient zeros out, and we don’t get to use this $(s, a)$ experience for gradient update even though this advantage is trying to force $π^{'} (a ∣ s)$ up.
If our advantage $A < 0$ and our ratio $r > 1 + ϵ$ then our gradient zeros out once again, and we miss utilizing this $(s, a)$ experience for parameter update, even though the advantage is telling us to force $π^{'} (a ∣ s)$ smaller.

Then our entire clipped objective adds a min term so that we only flattens the ratio on the side we care about!

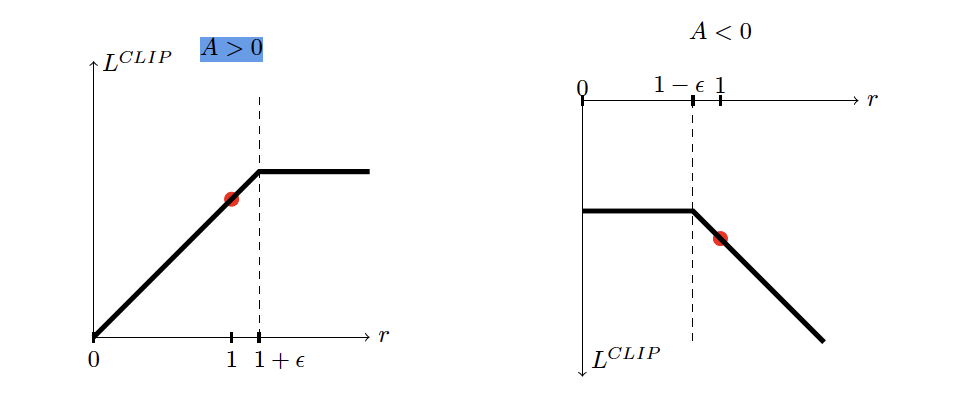
Asymmetric clipping

In reality we need to emphasize good actions when exploring for language models, meaning our clip term should be something like

c l i p (\frac{π^{'} (s ∣ a)}{π (s ∣ a)}, 1 - ϵ_{-}, 1 + ϵ_{+})

This means that we want to make $ϵ_{+} < ϵ_{-}$ so that we don’t clip for higher positive advantages that we would clip if we kept $ϵ_{-}$ fixed and had $ϵ_{+} = ϵ_{-}$ !

TRPO - Trust-Region Policy Optimization

If we were to keep the KL-constraint in our objective instead of a soft ratio-clipping objective with PPO, then the formulation is different. This is called TRPO.

Our surrogate objective is now

\begin{matrix} max_{θ} A_{π_{o l d}} (π) = \sum_{t = 1}^{T} E_{s_{t} \sim p_{θ_{o l d}} (s_{t})} E_{a_{t} \sim π_{θ_{o l d}} (a_{t} ∣ s_{t})} [\frac{π_{θ} (a_{t} ∣ s_{t})}{π_{θ_{o l d}} (a_{t} ∣ s_{t})} A^{π_{o l d}} (s_{t}, a_{t})] \\ s . t . E_{t} [D_{K L} [π_{θ_{o l d}} (\cdot ∣ s_{t}) ∥ π_{θ} (\cdot ∣ s_{t})]] \leq δ \end{matrix}